reads (since 2024-04-22)

My half-term project to compress audio files

!! Hey, go check out https://replit.com/@ysinkloucoll/halfterm-2023-10 !!

Over half-term break, I’ve been set work to do for each course I take at college, and for maths, that was to build some math-related project with Python.

Because of course I will take this opportunity to bite off far more than I can chew, let’s build a lossless audio codec!

Starting out: sampling and uncompressed audio

So, before we put pen to paper (keyboard to IDE?), I have to figure out how I intend to go about doing this.

So, let’s look at the “standards” that every major audio format seems to do.

First up: the raw data we’re working with, and definitions.

We record audio by using a series of samples. We take a snapshot of the continuous audio data at a given point, possibly round it to a convenient value (quantization), then store just those values.

Thanks to a fancy piece of math called the Nyquist-Shannon Sampling Theorem, we know that if we take a snapshot of the audio $f$ times per second, we can reproduce frequencies in the original audio source up to $\frac f 2$ Hz.

Why not above this frequency? Well, because above this frequency, the audio can oscillate one way and back again between two samples, so we have no way to know that it did so when we come to reconstruct the analog signal.

Can you see this problem in this diagram? The sampling frequency here is 1Hz, and the frequency of this sine wave is 0.8Hz.

Notice that the first two samples are both negative, and the second two samples both positive, the green wave shows what a reconstructed decoding would look like!

Frames

A “frame” is a concept that might seem more at place in graphics applications (it’s very intuitive what a frame means in the case of graphics - a single image to be displayed), frames are actually employed in the majority of audio formats too.

The idea is this: the characteristics of your audio change over time, and the amount of physical data taken up by a fixed time’s worth of audio may vary too, so frames make it viable to do two things:

Include regular metadata helping describe your data
- For example, MP3 uses this to tell the decoder how many decompressed samples are in this chunk of data
Allow efficent seeking, by breaking down the task of audio decoding from one file to one or more small chunks of audio.
- You can usually decode a very small number of frames alone, instead of the entire file at once
- And QOA uses this to re-set the weight for its least-mean-squares filter, to stop you from having to read the entire file in sequence just to play the end of it

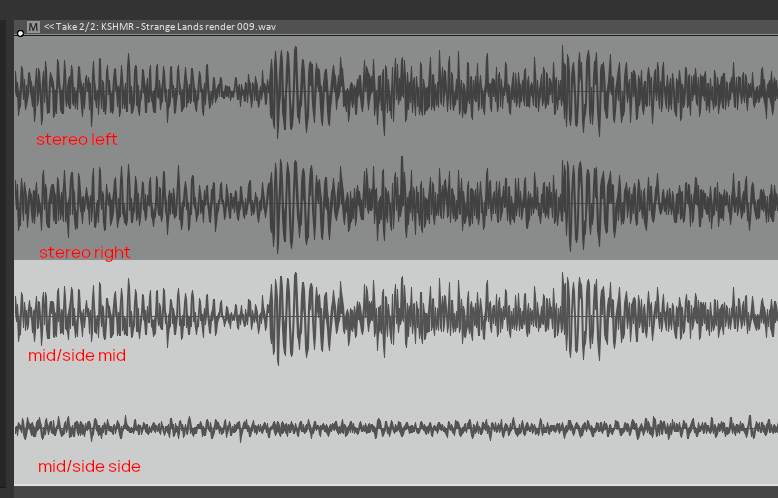
Simplifying the signal: Mid/Side

In most audio, the two audio channels are correlated - that is, the content of one channel is similar (but not identical to) the other.

Instead of compressing the same data twice, it can be a significant saving to store the difference between them.

The most common processing of this type in audio engineering is known as mid-side processing, in which, given left and right channels $L, R$ , you actually store $M=L+R, S=L-R$ .

You can then retrive the original data via the transform $L=\frac {M+S} 2, R=\frac{M-S} 2$ . If you work this out, it all adds up:

\frac {M+S} 2=\frac {L+R+L-R} 2 =\frac {2L} 2 =L

\frac {M-S} 2=\frac {L+R-L+R} 2 =\frac {2R} 2 =R

When we change to using mid/side encoding, notice that instead of storing two loud signals, we store one loud signal, and one much quieter signal. A quieter signal will compress better because it will use much smaller values that can be squashed together better.

Quick side note: A preference for small numbers

A common theme here will be aiming to make numbers we have to store as small as possible. In lossy codecs, this is good because once these numbers are small enough, we can throw them away.

Here, we are more interested in a neat property of numbers being small.

We need to remember that computers store numbers as binary. We may use a number system where each digit represents a power of ten, but for computers, its a power of 2. See this diagram, where we show the number on the bottom, as how many of each place value makes it up.

human:
  p.v.:  100 10 1
  count: 4   5  6
  value = (6 * 1) + (5 * 10) + (4 * 100) = 456

computer:
  p.v.:  256 128 64 32 16 8 4 2 1
  count: 1   1   1  0  0  1 0 0 0
  value = (1 * 8) + (1 * 64) + (1 * 128) + (1 * 256) = 456

Now, what happens if we have small numbers? Well, the digits to the left are 0, just like in decimal. More importantly though, computers store a fixed number of digits.

Here’s a standard 16 bit audio signal (though I’ve flipped the negative values back positive, for ease of visualization), with the point at which each digit becomes zero marked at the start, and the side signal too:

This is a VERY busy graph, but look closely at it a bit, and notice how the vast majority of the side signal is below the saves two bits line.

This is why we’re aiming for small values. If we can get VERY small values on the order of < 32, we can start packing the numbers incredibly, incredibly tightly, too!

(QOA, which is lossy, squashes its LMS residuals into 3 bits. That gives you SEVEN possible values. Not 65,536 like a 16-bit integer, no, SEVEN different values.) (its of course not that simple, but it is close enough.)

Actually compressing small numbers: Rice Coding

Rice coding is a technique that is used to use less bits for small numbers, while still being capable of encoding bigger ones.

Credit where due, the best explanation of this I found was on Monkey’s Audio, a well known and efficient lossless audio compressor.

Here’s what you do, to encode, let’s say, the answer to life, the universe, and everything, 101010:

Pick the number of bits you expect your data to use in general (call it $k$ ). Here, let’s say we expect our data to use about 4 bits on average.
Take your number in binary, and take the $k$ bottom bits and the remaining top bits separately. Here, the lower part is 1010 (=10) and the upper part is 10 (=2).
For the number represented by our upper bits, write zeroes - so write two zeroes.
Write a 1 to indicate that we’re done with our upper part.
Write the bits of the lower part directly.
So we get: 00 1 1010! Those gaps arent really there, its just one continuous stream of bits, but it aids visualization.

Lets do these steps in reverse to decode 110011 given that $k=5$ :

We encounter a 1 straight away! This means there are no leading zeroes, so the upper part is just 0
We read the next $K$ bits, which are 10011, or 19
This decodes to 19

You may ask why we need to know what $k$ is, since we can just count the zeroes then skip to the end of the value, surely, right?

Well, no, your data would actually be one continuous stream of bits with no alignment, you would have another value starting directly afterwards, so you need to know $k$ so you know how much to read, and when to stop reading.

When tested in practice, on LMS-compressed mid-side channels, on an average 3:30 16 bit audio file, this rice coding compresses the data down to about 80% of its uncoded size.

Don’t ask me why, because honestly I don’t know, but its worth noting that the optimal value of $k=log_2 (\bar x)$ , where $\bar x$ is the mean of your dataset. In most contexts, you would use the mean of the last few values, but in our case we do actually have all the data available to us ahead of time so we use the real mean.

Linear Sequence Compression: The Least-Mean-Squares Filter

The LMS filter was devised in 1960 by Bernard Widrow and Ted Hoff, and is a simplification of Gradient Descent, a common topic in the adjustment of Nerual Networks.

I like the LMS filter for prediction, because (as QOA appears to prove in practice), it can predict patterns in a sequence “well enough”, and is pretty easy to calculate.

I could start writing loads of equations and drawing diagrams here, but frankly, I don’t have a good grip on the more mathematical explanation of this filter, so I’ll show how it’d work given four states, in pseudocode.

We store two things: a history of the values we’ve seen last, and the weights of the filter.
Each value we see, predict the value using the current LMS state:
- Sum the products of each pair from the history and weights
  - $history_0 \times weights_0$
  - $history_1 \times weights_1$
  - You get the idea, sum these all up :)
- For four values, divide by $2^{13} = 8192$ .
- The difference between the sample $s$ and predicted $p$ is the residual $r$ .
Now, adjust the LMS state. First, the weights:
- The delta $d$ , the amount we adjust each weight by, is $\frac r {2^4=16}$
- For each weight $weights_n$ , if the corresponding $history_n$ is negative, then subtract the delta from that weight, else add the delta to that weight.
  
  (python: if (history[n] < 0): weights[n] -= delta; else: weights[n] += delta)
- Now, the history: just shift all the values left one, and add the real sample on the end:
  $[h_0, h_1, h_2, h_3] \rightarrow [h_1, h_2, h_3, s]$

Binary packaging format

Now we have compressed the data, we have the following things to work with:

LMS history and weights values for each frame
LMS residuals for each frame, rice coded
Rice coding $k$ value
Length of rice-coded buffer

We need to pack these efficently into a binary format.

I chose the following file structure:

file header, 16 bytes (fits neatly into two u64s or one xmm register!)

type	use	notes
`u32`	magic bytes	the ASCII for ‘SLAC’, sh---y lossless audio codec
`u8`	channels	always `0x02` for simplicity
`u24`	samplerate	Hz. Weird size but keeps alignment and big enough for 192,000
`u32`	frame count	assuming 1 frame = 4096 samples, at 44.1kHz gives max 12.64 years of audio
`f32`	compression ratio	nice to know, could in theory let decoders allocate the correct amount of RAM etc

then a stream of frames

frame header, 8 bytes (fits neatly into one u64)

type	use	notes
`u8`	mid rice $k$	The $k$ -value is necessary to decompress the rice decoding
`u8`	side rice $k$	As above
`u16`	mid rice length	The length is necessary to decompress. This is number of bytes, rounded up.
`u16`	side rice length	As above
`u16`	sample count	This can be worked out during the rice decoding process but helps pre-allocate arrays

LMS state for this frame, 40 bytes (decode into four u64s to get each part)
- 4x i24, LMS history for mid channel
- 4x i24, LMS history for side channel
- 4x i16, LMS weights for mid channel
- 4x i16, LMS weights for side channel
mid channel rice coded buffer containing LMS residuals, length given in header
side channel rice coded buffer containing LMS residuals, length given in header

Conclusion

This took a lot more work than I expected it to, but seeing it work the first time was, honestly, pretty awesome.

I can now compress audio data down to about 80% of its original size.

Doing so takes a bit over a minute on replit, 6.5 seconds on a 3.6GHz Ryzen 3200G, or 8 seconds on a 2.1GHz Ryzen 3500U. A Rust rewrite could probably go faster :)

(Take these frequency counts with a grain of salt, both chips use boosting to run faster depending on temperature etc.)

For reference, a FLAC file (at max compression) takes 0.993 seconds to encode on that 3500U and compresses to 76% size. I’ve not won!

If you’re only here because of this project, hi, this is my blog.

If you’re here because you know me, hi, this is a project I did for college (or rather, college is the excuse for it!)

Oh, by the way, the Mathematica notebook with all the diagrams and stuff is here.

Thanks