Proving the parabola of connected intervals

The exercise

There’s a very good chance you’ve done this activity before: take a worksheet like the one below, and connect equally spaced intervals with lines.

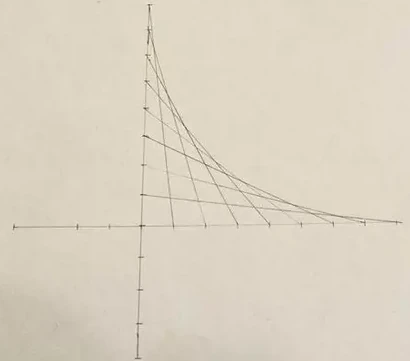
This, as you decrease the interval size, starts to resemble a curve, but which curve?

My motivation

Why am I here doing this?

Well, the other day my math teacher (in a math/coding activity thing the college run) was showing off this as a coding exercise, using p5js to make the computer draw this.

From there he asked what this curve might be, and we then spent a long chunk of time attempting to prove that it was a parabola.

I wanted to complete, tidy up, and present that proof, so here I am!

Let’s define the actual damn curve first

It’s all fun and games to construct approximations of curve out of lines, but we do need to actually have an idea of what the curve is.

So an important thing to notice here is that, if we take any of these ones lines (see the one in red!), the point on that line that we want to actually be a part of our curve is tangent to said curve.

Lets modify our construction just slightly so that we are constructing on diagonal lines, so each line will connect the points (k, k) and (k-n, n-k) for real k and constant n.

Finally, to allow us to increase n -> infinity, we need to add a scale factor of /n:

Notice that this construction is actually very very similar to DeCasteljau’s algorithm for computing Beziér curves.

In fact, if you look at this green line and think about its relation to the curve we want, you may notice that the point on the line that is on the curve moves from one end to the other.

As it turns out, this point is linear - therefore DeCasteljau’s construction of a quadratic Beziér perfectly works.

If we have Mathematica crunch down this construction into a nicer form, we get that the final construction is $f(t)= \left( \begin{matrix} 2t-1 \\ 2t^2-2t+1 \end{matrix} \right)$.

Finally, let’s convert this from a parametric equation in terms of t into a y-x equation:

$x=2t-1 \Leftrightarrow t=\frac{x+1}{2}$

$y=2t^2-2t+1$
$y=2 (\frac{x+1}{2})^2 -2 \frac{x+1}{2} +1$

$y=\frac{x^2+1}{2}$

So there it is, a parabola from the construction! Specifically, $\frac{x^2}{2} + \frac{1}{2}$.

Hope to see ya back here soon
— Yellowsink